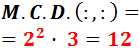PROBLEMAS mcm - MCD
Problema 6
Simón tiene una pista de carreras con dos autos. El primer auto le da una vuelta completa a la pista en 31 segundos y el segundo lo hace en 17 segundos.
Carlos también tiene su pista de carreras con dos autos, pero el primero da una vuelta completa en 36 segundos y el segundo en 42 segundos.
Como Carlos siempre pierde cuando juegan, propone a Simón que el ganador sea quien tenga en su pista sus dos autos situados en la meta al mismo tiempo. ¿Quién ganará?
Solución
Primero calculamos, en cada pista, cuándo coinciden los dos autos. Para ello, calculamos el m.c.m. de los tiempos. Después, comparamos los tiempos para saber cuál es menor.
Calculamos el m.c.m. de los tiempos de los autos de Simón:
El m.c.m. se calcula multiplicando los factores «comunes y no comunes al mayor exponente»:
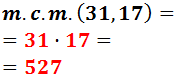Por tanto, en la pista de Simón los autos coincidirán en la meta cada 527 segundos.
Ahora repetimos el proceso para los autos de Carlos:
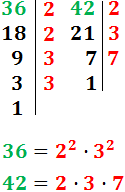El m.c.m. se calcula multiplicando los factores «comunes y no comunes al mayor exponente»:
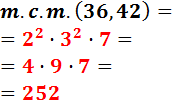Por tanto, los autos de Carlos coincidirán en la meta cada 252 segundos.
Luego Carlos ganará porque sus autos coincidirán en la meta antes que los de Simón.
Nota: los tiempos de Simón son mejores que los de Carlos, pero como son números primos, no tienen factores comunes y su m.c.m. es un número mayor.
Calculamos el m.c.m. de los tiempos de los autos de Simón:
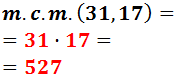
Ahora repetimos el proceso para los autos de Carlos:
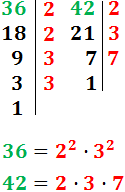
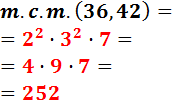
Luego Carlos ganará porque sus autos coincidirán en la meta antes que los de Simón.
Nota: los tiempos de Simón son mejores que los de Carlos, pero como son números primos, no tienen factores comunes y su m.c.m. es un número mayor.
Problema 7
Máximo quiere pintar una casa pequeña. Según sus cálculos, necesitará 12 litros de pintura roja, 24 litros de pintura verde y 16 litros de pintura blanca. Pero quiere comprar botes de pintura que tengan la misma cantidad de litros y que el número de botes sea el menor posible, ¿de cuántos litros debe ser cada bote y cuántos botes de cada color debe comprar Máximo?
Solución
Las sumas de los litros de los botes de color rojo, verde y blanca deben ser 12, 24 y 16, respectivamente. Como todos los botes deben tener la misma capacidad, dicha capacidad debe dividir a 12, 24 y 16. Además, como quiere tener la mínima cantidad de botes, cada bote debe tener capacidad máxima. Por tanto, tenemos que calcular el M.C.D. de 12, 24 y 16.
Factorizamos los números:
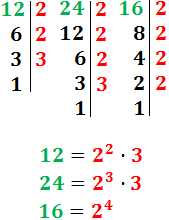El M.C.D. se calcula multiplicando los factores «comunes al menor exponente»:
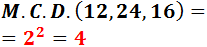Por tanto, cada bote debe tener una capacidad de 4 litros.
Para calcular cuántos botes de cada color necesita Máximo, sólo tenemos que dividir entre 4:
Botes de pintura roja:
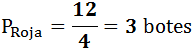Botes de pintura verde:
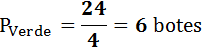Botes de pintura blanca:
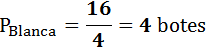
Factorizamos los números:
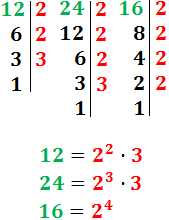
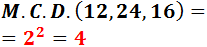
Para calcular cuántos botes de cada color necesita Máximo, sólo tenemos que dividir entre 4:
Botes de pintura roja:
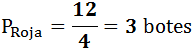
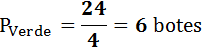
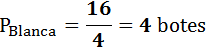
Problema 8
Un sitio turístico en el Caribe ofrece tres diferentes cruceros: uno tarda 6 días en ir y regresar a su punto de inicio, el segundo tarda 8 días y el tercero tarda 10 días. Si los tres cruceros partieron al mismo tiempo hace 39 días, ¿cuántos días faltan para que vuelvan a partir el mismo día todos los cruceros?
Solución
Calculamos el m.c.m. para saber cada cuántos días los cruceros coinciden. Aunque tenemos tres números en lugar de dos, el procedimiento es el mismo.
Factorizamos los números:
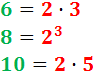El m.c.m. se calcula multiplicando los factores «comunes y no comunes al mayor exponente»:
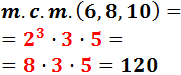Por tanto, sabemos los tres cruceros parten a la vez que cada 120 días. Pero como la última vez que coincidieron fue hace 39 días, la próxima coincidencia será dentro de
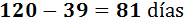
Factorizamos los números:
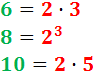
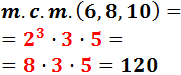
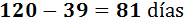
Problema 9
Daniel y Matías compraron 40 y 32 caramelos, respectivamente, para una fiesta de cumpleaños. Quieren repartirlos entre todos los invitados de modo que cada uno da el mismo número de caramelos a cada persona, pero que todos los invitados tengan el mismo número de caramelos y sea máximo.
Calcular el número máximo de invitados que deben asistir para que ninguno se quede sin caramelos.
Solución
Como Daniel y Matías deben dar el mismo número de caramelos a cada persona, dicho número debe ser divisor de sus respectivas cantidades de caramelos. Además, como la cantidad debe ser máxima, tenemos que calcular el M.C.D.
Factorizamos los números:
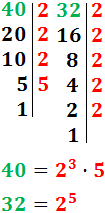El M.C.D. se calcula multiplicando los factores «comunes al menor exponente»:
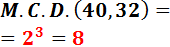Por tanto, el número de caramelos por persona es 8. Para saber a cuántas personas pueden invitar, debemos sumar las cantidades de caramelos y dividirlas entre el M.C.D.:
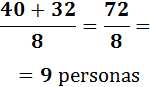
Factorizamos los números:
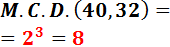
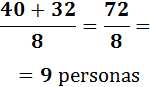
Problema 10
Juan, Paul, David y Andrea van a correr a un parque todos los días. Juan le da una vuelta al parque en 2 minutos, Paul le da 3 vueltas al parque en 7 minutos con 30 segundos, David le da 4 vueltas en 9 minutos con 20 segundos y Andrea le da 2 vueltas al parque en 4 minutos con 20 segundos.
Si todos parten al mismo tiempo y del mismo lugar, contestar:
- ¿Quién es el más y el menos veloz?
- ¿Cuánto tardarían en encontrarse todos en el punto de partida?
Solución
Como los tiempos están en minutos y en segundos, lo primero que haremos es escribirlos en segundos.
Juan tarda 2 minutos en dar una vuelta, es decir, su tiempo es de
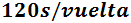Paul tarda 7 minutos y 30 segundos en dar tres vueltas. Este tiempo en segundos es
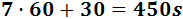Luego su tiempo es de
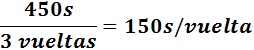David tarda 9 minutos y 20 segundos en dar 4 vueltas. En segundos,
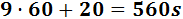Luego su tiempo es de
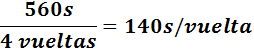Andrea tarda 4 minutos y 20 segundos en dar 2 vueltas. En segundos,
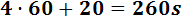Luego su tiempo es de
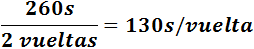Con lo que tenemos, ya podemos saber que el más veloz es Juan y el menos veloz es Paul.
Cada uno de los atletas se encuentra en la salida cuando ha pasado el tiempo que tarda en dar una vuelta completa. Por tanto, el tiempo en el que los cuatro se encuentran en la salida es un múltiplo común de los tiempos. Como queremos saber la primera vez que esto ocurre, calculamos el mínimo de los múltiplos. Luego debemos calcular el m.c.m.:
Descomponemos los números:
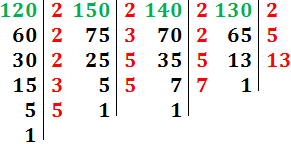El m.c.m. se calcula multiplicando los factores «comunes y no comunes al mayor exponente»:
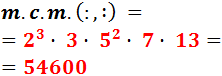Escribimos los segundos en minutos:
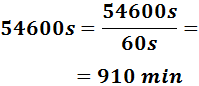Es probable que dejen de correr antes de que lleguen a encontrarse en la meta porque difícilmente estarán 910 minutos seguidos corriendo.
Juan tarda 2 minutos en dar una vuelta, es decir, su tiempo es de
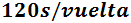
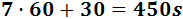
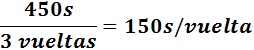
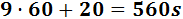
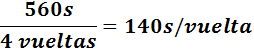
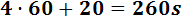
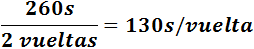
Cada uno de los atletas se encuentra en la salida cuando ha pasado el tiempo que tarda en dar una vuelta completa. Por tanto, el tiempo en el que los cuatro se encuentran en la salida es un múltiplo común de los tiempos. Como queremos saber la primera vez que esto ocurre, calculamos el mínimo de los múltiplos. Luego debemos calcular el m.c.m.:
Descomponemos los números:
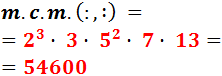
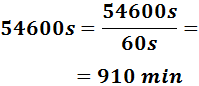
Problema 11
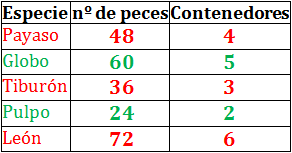
Un acuario pequeño se quedó en bancarrota, por lo que otros acuarios van a comprar los peces que tienen. En total, se venderán 48 peces payaso, 60 peces globo, 36 tiburones bebés, 24 pulpos y 72 peces león.
Para la venta, se desea que los contenedores sean del mismo tamaño y que alberguen la mayor cantidad de animales posible. Además, en cada contenedor sólo puede haber peces de una única especie.
¿Cuántos peces debe haber por contenedor y cuántos contenedores se necesitan para cada especie?
Solución
Como en cada contenedor sólo puede haber una especie, el número de peces que hay en cada contenedor debe dividir al número total de peces de cada especie. Además, debe ser máximo.
Por tanto, debemos calcular el M.C.D. de las cantidades de peces.
Descomponemos los números:
El M.C.D. se calcula multiplicando los factores «comunes al menor exponente»:
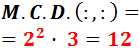Para saber cuántos contenedores para cada especie se necesitan, dividimos la cantidad de animales de cada especie entre la capacidad de los contenedores:
Por tanto, debemos calcular el M.C.D. de las cantidades de peces.
Descomponemos los números:
